[BOJ6549] 히스토그램에서 가장 큰 직사각형

[BOJ6549] 히스토그램에서 가장 큰 직사각형

문제 링크

---

문제 설명

• 이 문제는 히스토그램(막대그래프)가 길게 나열되어있고, 그 안에 있는 직사각형의 최대 넓이를 구하는 문제이다. (아래 그림 참고)
• 막대의 개수 n의 범위는 1~100,000 이고, 막대의 높이는 0~1,000,000,000 까지이다.
• 각 칸의 넓이는 1.

---

코드 구성

• 모든 경우의 수를 다보아도 되지만, n의 범위를 보았을 때 답을 1초안에 낼 수는 없다.
• 쿼리에 대한 방법 을 떠올려야 한다.
• 모든 막대그래프를 먼저 배열에 넣는다.
• 뒤에 부분을 구현하기 위하여 먼저, 세그먼트 트리 를 만든다.
• 노드의 값으로는 먼저 그 구간에서 최소 높이를 가지고 있는 막대그래프의 인덱스 번호 를 넣는다.
• 리프 노드는 그 개개의 막대 그래프의 인덱스 번호 를 넣는다.
• 리프 노드를 제외한 노드에는 그 노드 하위에 있는 노드들의 인덱스 범위 구간에 있는 최소 높이를 가지고 있는 막대그래프의 인덱스 번호 를 계속해서 넣어간다.

• 0 ~ n-1구간에 대해 가장 높이가 낮은 막대그래프를 찾고, 그 높이를 가지고 있는 최대 직사각형을 그리면 가로의 길이: n, 높이: 뽑은 막대그래프의 높이 가 된다. (아래 그림 참고)

• 이 경우가 선택한 막대그래프를 포함하여 그릴 수 있는 직사각형의 최대 넓이 가 된다.
• 그 후 분할 정복 을 통해 선택했던 막대그래프를 제외한 왼쪽 부분과 오른쪽 부분으로 나누어 앞앞 과정 을 재귀적으로 반복 한다.

• 왼쪽 범위에서 고른 직사각형 최대 넓이, 오른쪽 부분, 그리고 가운데 막대그래프를 선택했을 때 그렸던 직사각형 넓이 3개를 비교하여, 최대를 선택 한다.

---

코드 리뷰

• 세그먼트 트리를 통한 문제는 처음 풀어봐서 어떻게 풀어야할지 처음엔 감조차 안왔다.
• 이해하고, 푸니깐 엄청나게 어렵진 않았지만, 여러 문제를 통해 연습을 해야할 것 같다.
• 더 깔끔한 코드를 구현하게 되면 새로 추가할 예정.

---

#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>

#define RANGEOUT -4444
using namespace std;

int repeat_func(vector<int> &stick, vector<int> &segtree, int node, int start, int end, int left, int right) { //쿼리작업
	//구하고자 하는 범위는 left~right , start와 end로 구간 나눔
	if (left > end || right < start)	return RANGEOUT;
	if (left <= start && end <= right)	return segtree[node];
	int left_ans = repeat_func(stick, segtree, node * 2, start, (start + end) / 2, left, right);
	int right_ans = repeat_func(stick, segtree, node * 2 + 1, (start + end) / 2 + 1, end, left, right);
	if (left_ans == RANGEOUT) return right_ans;
	if (right_ans == RANGEOUT) return left_ans;
	if (stick[right_ans] >= stick[left_ans]) return left_ans;
	else return right_ans;
}

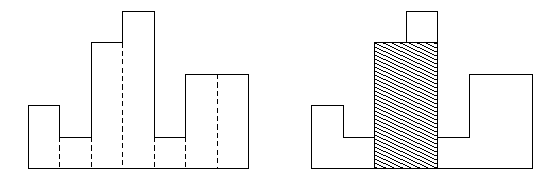
long long Max_Rectangle(vector<int> &stick, vector<int> &segtree, int left, int right) {
	int min_idx = repeat_func(stick, segtree, 1, 0, stick.size() - 1, left, right); // 쿼리를 통해 그 구간에 대한 최소 높이 막대 인덱스 가져옴
	long long area = (long long)(right - left + 1) * (long long)stick[min_idx];
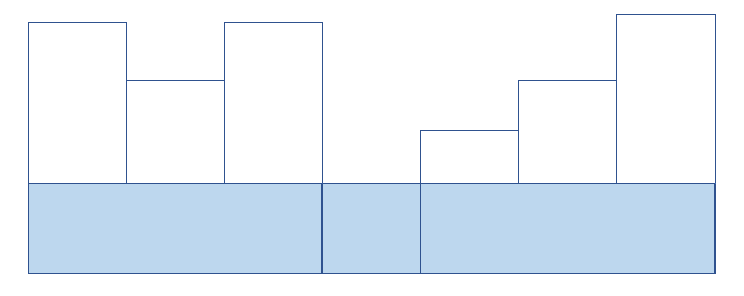
	if (left <= min_idx - 1) { //최소높이 찾은 막대기 인덱스 왼쪽에 아직 스틱들이 존재하면 분할정복
		long long left_area = Max_Rectangle(stick, segtree, left, min_idx - 1);
		area = max(area, left_area);
	}
	if (right >= min_idx + 1) {//최소높이 찾은 막대기 인덱스 오른쪽에 아직 스틱들이 존재하면 분할정복
		long long right_area = Max_Rectangle(stick, segtree, min_idx + 1, right);
		area = max(area, right_area);
	}
	return area; // 최대 넓이 반환
}

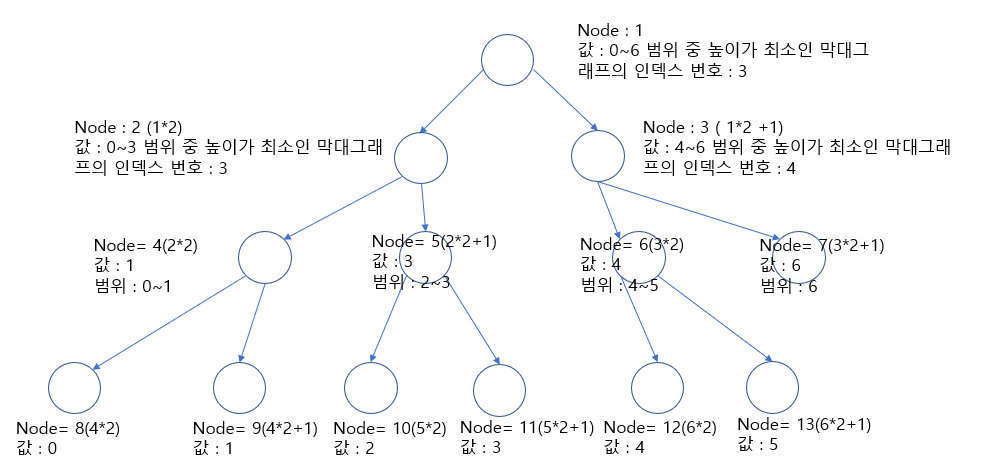
void make_seg(vector<int> &stick, vector<int> &segtree, int node, int start, int end) {
	if (start == end) {//start와 end 즉 구간이 점으로 바뀌면 리프노드에 있는 그 자체 인덱스가 된다.
		segtree[node] = start;
		return;
	}
	// start와 end가 다른 경우(리프노드가 아닌 경우)
	make_seg(stick, segtree, node * 2, start, (start + end) / 2);
	make_seg(stick, segtree, node * 2 + 1, (start + end) / 2 + 1, end);
	// 각 구간에서 가장 높이가 낮은 스틱의 인덱스를 세그먼트 트리 노드에 넣어준다.
	if (stick[segtree[node * 2]] <= stick[segtree[node * 2 + 1]]) segtree[node] = segtree[node * 2];
	else segtree[node] = segtree[node * 2 + 1];
}

int main() {
	int n;
	scanf("%d", &n);
	int tree_h = 0;
	if (log2(n) == (int)log2(n)) tree_h = (int)log2(n);
	else tree_h = (int)log2(n) + 1;
	vector<int> stick(n);  //히스토그램의 높이가 저장된 배열
	for (int i = 0; i < n; i++) scanf("%d", &stick[i]);
	int tree_size = (int)pow(2, tree_h + 1); //세그먼트 트리 최대 사이즈
	vector<int> segtree(tree_size); //세그먼트 트리를 만들기 위한 배열 -> 값으로는 arr의 인덱스번호가 들어감
	make_seg(stick, segtree, 1, 0, n - 1); // 세그먼트 트리 형성
	long long result = Max_Rectangle(stick, segtree, 0, n - 1);
	printf("%lld\n", result);
	return 0;
}

---