[알고리즘설계] Bin-Packing

3 분 소요

Bin-Packing 문제는 대표적인 NP문제 이기 때문에, 휴리스틱을 사용하여 근접한 답을 내는 방법과, Bin-Packing 문제 자체에 조건을 추가하여 실제 답에 근사한 답으로 접근하는 방법 두가지에 대해 포스팅 하려한다.

Bin-Packing 문제를 보기전에 먼저 대비되는 문제인 Knapsack Problem 에 대해 알아보자.
배낭 문제는 두가지가 존재하는데, fractional Knapsack (분할 가능 배낭 문제) 와 0-1 Knapsack(제로원 배낭문제) 가 있다.
분할 가능 배낭 문제는 배낭에 넣을 수 있는 최대 무게가 N이라고 하고, 공들의 무게가 w1,w2,w3 … wi로 존재하며 배낭에 공들을 넣을 때, 공 한개의 무게를 쪼개서도 넣을 수 있다. 이때 가치의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제이다.
제로원 냅색 문제는 공들을 쪼갤 수 없어서 공을 가방에 넣느냐 마느냐로 가치의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제이다.
분할 가능 배낭 문제는 그리디 알고리즘을 통해 다항시간안에 해결할 수 있는 반면 제로원 냅색은 DP로 풀 수 있지만, NP-complete라 다항시간에 풀 수 있진 않고, 다항시간 근사 해법은 존재한다.

가방에는 1개 혹은 2개의 물건만 넣을 수 있다는 조건이 추가된 문제를 푼다.
w = {4,3,8,2,4,5,8,6} 이고, M= 12 로 설정된 문제를 예시로 풀어보자.
1. 먼저 w를 정렬한다 - 2,3,4,4,5,6,8,8 (O(nlogn))
2. 제일 큰 값(w)은 무조건 상자에 넣는다. 그 후, 제일 작은 값(w) 를 M-8과 비교해서 넣을 수 있으면 넣고 (남은 w개수 n-2), 못 넣으면 최대값만 넣은 상태로(남은 w개수는 n-1) 남은 개수들에 대해 반복 진행을 한다.
주장은 최대값을 넣고 최소값 들어가면 넣고 안들어가면 안넣고 나머지에 대해 다시 풀면 된다는 것 인데, 우려는 위의 예시로 봤을때, 8,2가 아닌, 8,4를 넣어야 하는 것 아닌가? 라는 점이다.
하나의 가방(A)에 8,4를 넣었다고 할 때, 2는 분명 어떤 다른 가방(B)에 들어가 있을 것이다.
8과 함께 들어가 있는 다른 무게(y)는 예시에선 4로 했지만, 2보다는 크거나 같은 값이 들어갈 것이다. 즉 y>=2
그리고 2와 함께 들어가 있는 다른 무게(z) 는 분명 8보다는 작거나 같은 값이 들어갈 것이다. 즉 z<=8.
그렇다면, y와 2를 바꿔도 8+2 <=12 이고, z+y<=12가 성립하게 되어, (8,2)를 고르는 방식이 항상 옳다는 것 을 알 수 있다.
시간 복잡도는 정렬을 한 후, 모든 원소를 한번씩 다 보면서 넣는 것이므로 O(nlogn)+O(n) 이므로 O(nlogn) 이 된다.

best-fit 과 worst-fit 방법 이 있다. 두 방법 다 정렬을 하지 않고, 새로 무게 하나를 넣고, 다음 무게가 기존 상자에 들어가면 넣고, 안들어가면 새로 상자 하나 만들어서 넣는 것 까지는 공통적으로 진행된다.
무게 w = {4,3,8,2,4,5,8,6,5,7,8,6}
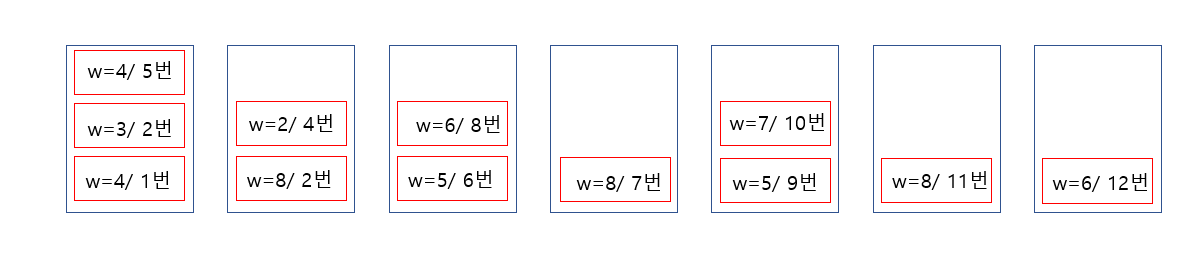
아래 그림에서 빨간 물건 왼쪽에 써있는 것은 무게, 오른쪽에 써있는건 위의 원소에서 몇번째인지를 나타낸 것이다.
이 때 아래 그림은 best- fit 으로, 새로운 것을 넣을 때, 남아있는 공간이 조금 더 큰 공간을 아끼는 방식이다. 1번, 2번, 3번 물건까지는 best-fit과 worst-fit이 똑같이 들어가는데, 4번 무게 2짜리 물건을 넣을 때, best-fit은 첫번째 가방과 두번째 가방 중 남아있는 공간이 더 작은 2번가방에 넣게 되는 것이다.
이 방식대로 하면 아래 그림처럼 총 7개의 가방이 필요하게 된다.
하지만 첫번째 가방에 있는 물건들을 4,6,7번째 가방에 각각 나눠 넣으면, 가방의 수를 줄일 수 있다. 이 부분이 휴리스틱 방식에서 오는 오차이다.

하나의 무게를 집어 넣을 때, 앞에 있는 모든 값들을 탐색해야 한다. 또한 모든 원소가 그 작업을 반복하므로, 최악의 경우 O(n^2) 시간이 걸린다. 휴리스틱 방식인데 O(n^2) 시간복잡도 를 가지고 있는 것은 엄청 성능이 안좋다고 해도 과언이 아니다.
한 원소를 봤을 때, 앞에 있는 상자의 남은 용량이 이 원소보다 크면서, 그 중 사이즈가 작은 것을 골라야 하는데, 매 원소마다 넣고 정렬을 한다면, O(n^2)보다 아래로 시간을 줄일 수 없다.
삽입 연산과 탐색이 용이하면서, 삭제연산도 가능하고, 완벽히 정렬이 되어있진 않지만 느슨한 상태인 자료구조를 사용하면 되겠다는 아이디어 를 생각해야 한다.
이진 탐색 트리 중에서 BBST 를 사용하면 된다. (키는 남아있는 용량)

Bin-packing 문제는 NP문제이기 때문에 휴리스틱을 이용하여 근사한 답을 찾아내거나, Bin-packing 문제 자체에 조건을 넣어 특수한 상황에서의 Bin-Packing 문제를 풀어 볼 수 있다.

[BOJ12886] 돌 그룹