[알고리즘 설계] 다익스트라 알고리즘
이번 포스팅에서는 최단 경로(Shortest Path)를 찾는 알고리즘들 가운데 하나인 다익스트라 알고리즘(Dijkstra’s Algorithm)에 대해 작성하려 한다.
최단 경로
최단 경로문제는 정점 u와 정점 v를 연결하는 경로 중 간선들의 가중치 합이 최소가 되는 경로를 찾는 문제다.
가중치는 가중치 인접 행렬이라고 불리는 2차원 배열에 저장된다.
가중치 인접행렬과 기존 인접행렬에는 약간의 차이점이 있는데, 기존의 인접행렬에서는 간선이 없는 구간에는 행렬의 값을 0으로 표기하였었지만, 가중치 인접행렬에서는 간선의 가중치 자체가 0일 수도 있기 때문에 간선이 없음을 나타낼 때 이론적으로 무한대의 값을 저장한다.

Dijkstra의 최단 경로 알고리즘
다익스트라 알고리즘은 그래프에서 하나의 시작 정점으로부터 모든 다른 정점까지의 최단 경로를 찾는 알고리즘이다.
기본적으로 다익스트라 알고리즘의 아이디어는 최단 거리는 최단 거리로 이루어져 있다 라는 그리디한 생각에서부터 출발한다.
다익스트라 알고리즘에서는 최단 거리에 해당하는 정점이 하나씩 추가되는 집합 S에 있는 정점만을 거쳐서 다른 정점으로 가는 최단 거리를 기록하는 배열이 있어야 한다. 또한 후보가 될 수 있는 간선 중 최고로 작은 간선을 빠르게 뽑아낼 수 있는 힙 자료구조가 필요하다.
이 포스팅에서는 최단 거리를 기록하는 1차원 배열을 distance 배열이라고 부르겠다.
시작정점을 v라고 했을 때, distance[v]=0이고, 다른 정점에 대한 distance 값은 시작 정점과 해당 정점 간의 가중치가 된다. 가중치는 인접 행렬에 저장되므로 가중치 인접 행렬을 weight라고 했을 때, distance[w] = weight[v][w]와 같이 사용할 수 있다.
단 정점 v에서 w로의 직접 간선이 없을 경우에는 초기에 무한대의 값을 저장한다. 알고리즘이 진행되면서 최단 거리가 발견되는 정점들이 S 집합에 하나씩 추가 될 것이다.
과정
시작 정점을 0으로 잡았다고 생각하고 과정을 나타내보겠다.
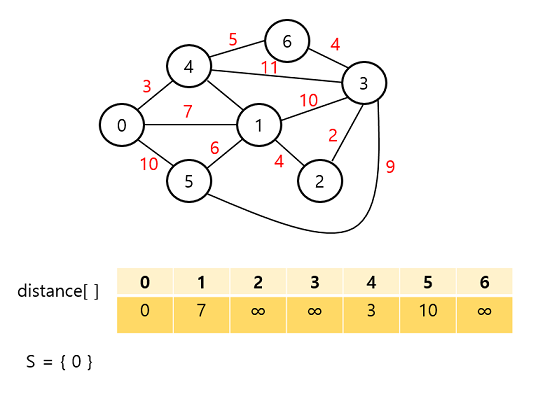
시작 정점을 0으로 잡고, 각 정점까지의 거리를 표시했다. 직접적으로 가는 경로가 없는 경우 무한대로 표시한다.
이때, 표시되어 있는 거리 중 가장 짧은 거리는 정점 4까지의 거리인 3이므로 정점 4를 추가한다.
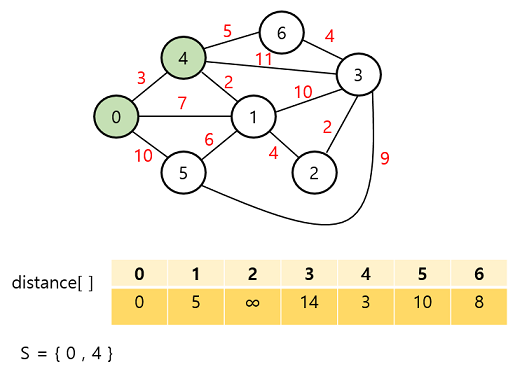
새로운 정점이 S에 추가되면 다른 정점들의 distance 값이 변경된다. 0번 정점에서는 직접적으로 갈 수 없던 정점에 새롭게 들어온 4번 정점을 통해 갈 수 있기 때문에 값이 갱신된다.
또한, 새로운 정점 4를 통해 갈 때 더 짧은 경로가 발견되면 그 정보 또한 갱신한다.
이제 남은 정점 중 가중치가 가장 적게 표시 된 정점은 1번 정점이다.
1번 정점을 S에 추가하고 아까와 마찬가지로 값을 갱신해준다.
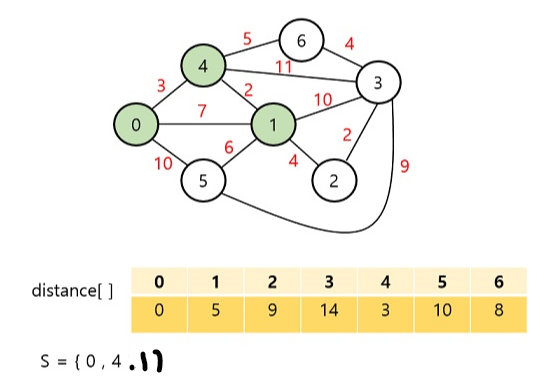
이후엔 정점 2가 추가될 것이고, 5번, 3번 순으로 진행될 것이다.
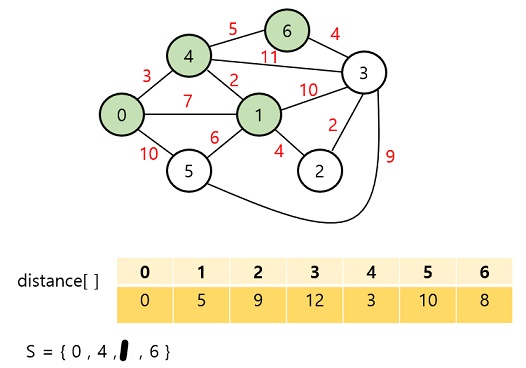
출처
(화투의 개발 블로그)[https://hsp1116.tistory.com/42]
(
댓글남기기