[알고리즘설계] Interval Graph - 1 (Scheduling)
[알고리즘 설계] Interval Graph - 1 (Scheduling)
문제
-
영화배우가 ‘한편의 영화당 촬영의 시작과 끝’ 을 알고 있을 때, 촬영할 수 있는 영화의 최대 개수 를 구하는 문제이다.
-
구간이 겹치는 영화들은 선택할 수 없다.
-
입력은 N개의 영화의 시작과 끝이 주어진다.
문제를 풀기위하여 생각해 볼 수 있는 방법들
1. Shortest Interval (가장 구간이 짧은 영화들을 우선적으로 선택)
- 최적의 해가 보장되는 알고리즘이 없을 경우 선택한다 (휴리스틱).
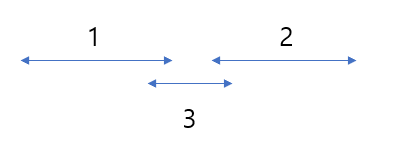
-
반례 존재.
-
Shortest Interval 아이디어를 이용하여 풀게되면 위와 같은 상황에서 3번 스케쥴을 우선적으로 선택하게 된다.
2. Eariest Left Endpoint (영화의 시작점이 가장 왼쪽에 있는 영화를 우선적으로 선택)
- 역시 최적의 해가 보장되는 알고리즘이 없을 경우 선택한다 (휴리스틱).
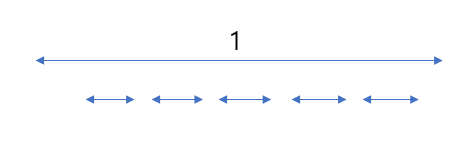
-
반례 존재.
-
Eariest Left Endpoint 아이디어의 경우 위와 같은 상황에서 1번 스케쥴을 우선적으로 선택하게 되어 틀린 답이 나오게 된다.
3. Eariest Right Endpoint (영화가 끝나는 점이 가장 왼쪽에 있는 영화를 우선적으로 선택)
- 최적 보장 (알고리즘) .
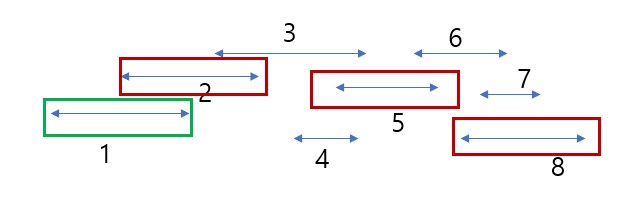
-
결론부터 말하면 최적인 해에는 오른쪽 끝 점이 가장 작은 구간을 반드시 포함하게 된다.
-
2,5,8 구간을 선택할 때, 2대신 1을 선택해도 상관 없다 (즉, 1은 무조건 포함하고, 나머지를 적절히 선택하면 된다).
Eariest Right Endpoint를 기준으로 푸는 방법들중 최적의 방법 찾기 (시간복잡도 기준)
1. 첫번째 방법 (시간복잡도: O(n^2))
-
탐색을 통해 오른쪽 끝점이 가장 왼쪽에 있는 구간 을 찾는다.
-
선택한 구간을 기준으로 겹치는 구간을 탐색을 통해 찾는다(최악의 경우 겹치는 구간 없음).
-
나머지 구간들을 대상으로 다시 1,2를 실행한다(Recursion).
- T(n) = O(n) + T(n-1) = O(n^2)
2. 두번째 방법 (시간복잡도: O(n^2)) : 정렬을 하고 풀기
-
오른쪽 끝점을 기준으로 정렬 을 했으므로 제일 왼쪽 구간을 선택 한다.
-
왼쪽점이 1구간보다 왼쪽에 있는 구간들 제거 (겹치는 구간)
-
나머지를 대상으로 1,2 다시 진행.
-
첫 구간 기준으로 n-1개 확인해야 하고, 두번째 구간 기준으로 n-2개 확인해야 한다…..(겹치는 지 확인), n-1번째 구간을 기준으로 1개 확인해야 한다.
-
T(n)= O(nlogn) + O(n^2) = O(n^2)
3. 세번째 방법 (시간복잡도: O(nlogn))
-
첫번째 방법과 두번째 방법은 하나의 구간을 고르고, 교차하는 구간 지우고, 나머지 구간들에 대해 다시 진행 하는 방식이었다. 세번째 방법은 하나의 구간을 고르고, 다음 구간을 봐서 겹치면 넘어가고, 안겹치면 선택하는 방식으로 진행된다. (n번 안에 처리된다.)
-
즉, 오른쪽 끝점을 기준으로 정렬을 한 후 맨 앞 구간부터 보면서 겹치면 지우고, 안겹치면 선택하는 방식이므로 T(n) = O(nlogn)+ O(n) = O(nlogn) 에 처리할 수 있게 된다.
-
한가지 고민해봐야 할 부분이 만약 아래의 그림에서 3번 구간을 확인해야 하는 상황이고, 그 전 구간인 2번 구간을 기준으로 2번과 겹치는 지를 보는 거라고 가정할 때, 1번 구간과 겹치는지도 확인해봐야 하지 않을까? 라는 점이다.
- 이에 대한 해답은 직관적으로 생각해보면 된다.
- 2번 구간을 기준으로 3번 구간을 확인해보는 중이라 할 때, 2번 구간이 선택되었다는 것은 1번 구간과 겹치지 않았기 때문에 선택하게 된 것일 것이다. 그렇다면 정렬이 된 상태에서, 1번과 2번구간이 겹치지 않는다는 것을 이미 알고 온 것이고, 또한 3번이 2번과 겹치는지를 확인 할때 2번과 겹치지 않는다면 당연하게도 1번과 겹치지 않을 것이고, 2번과 겹친다해도 역시 1번과는 겹치지 않을 것이다.
- 그렇기 때문에 전전단계를 확인할 필요가 없이 전 단계 만 비교하면 된다.

결론
- 위의 문제에 해당하는 Interval Scheduling 방법에는 O(nlogn) 시간안에 구할 수 있는 알고리즘 이 존재한다.
- 틀린 부분이 존재할 수 있으니 참고해주시기 바랍니다.
댓글남기기