[알고리즘설계] 가중치가 주어지는 Interval Graph
[알고리즘 설계] 가중치가 주어지는 Interval Graph (Weighted Independent Set)
Binary Search Tree 간략한 설명
-
탐색할 때 사용, 리스트를 정렬한 후 이진 탐색을 하게 될때의 단점은 삽입, 삭제가 있다.
-
BST는 부분적으로 정렬을 해놓은 모양이라 최악의 경우 O(n) 시간에 정렬을 할 수 있다. BST의 부분적 정렬은 정렬에 상당히 가까운 느슨한 정렬 상태이다.

Balanced Binary Search Tree 간략한 설명
- BST는 기준이 노드 중심으로 왼쪽이 작은 값, 오른쪽이 큰값이라 좌우 개수가 최악의 경우 심할 수 있다.
- 기준이 좌우개수가 비슷하게 만든 트리가 BBST.
- ex) 레드블랙트리/ AVL트리
- O(logn) 에 처리할 수 있다. 이진탐색트리보다는 조금 더 시간이 걸릴 수 있다.
Weighted Independent Set (가중치가 주어지는 Interval Graph)
- 앞에서 푼 인터벌 스케쥴링 문제에 구간마다 가중치가 주어지는 경우이다.
- 예로 들자면, 영화 한편당 받을 수 있는 수당등이 주어지는 경우가 있다.
- 영화 수익을 최대로 낼 수 있게 찍는다고 하면? Max Weighted Independent Set
- 구간을 정점으로 두고, 겹치지 않는 정점 방향으로 화살표를 준다.(아래 그림 참고) -> 방향 그래프 만들어진다.
- 경로 개념과 독립집합 개념이 맞아 떨어진다.
- 정점에 있는 가중치의 합은 경로의 길이가 된다. => ‘경로가 가장 긴 것을 찾아라’ => Longest Path Problem 문제 (최장 경로 문제).

Longest Path Problem
- 방향 그래프 문제에서 최장 경로 문제를 구하는 것은 NP complete 문제.
- 하지만 위의 경우는 방향 그래프 중 특수한 경우.
- 사이클이 생기지 않는 방향 그래프이다. 즉, DAG(Directed Acyclic Graph) .
- DAG 에서는 최장 경로 문제를 빠르게 구할 수 있다.
DAG
- 비순환 유향 그래프인 DAG은 위상 정렬을 통해 정렬 을 한다.
- 위상 정렬(조건은 비순환 유향 그래프여야 한다.) -> 방향 그래프의 정점들을 간선의 방향을 거스르지 않게 정렬을 하는 것 .

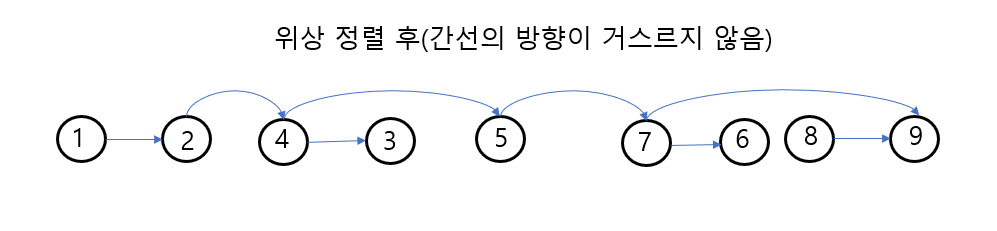
에지에 가중치가 있는 그래프 - 동적계획법으로 풀기
- 정점에 가중치가 있는 문제를 풀기 전에 에지에 가중치가 있는 그래프를 먼저 해보겠다.
- 위상 정렬이 되어있는 에지에 가중치가 있는 그래프를 가지고, 각 점에서 끝나는 제일 긴 것들을 찾아나가는 식으로 디피 배열을 만든다.
- 한 점의 디피 배열에 저장되는 값은, 그 점에 연결되어있는 indegree들을 보면 된다. 그 점에 연결된 indegree를 outdegree 삼고있는 배열의 값들에 indegree 즉 에지에 있는 가중치를 더한 값 이 가장 큰 값을 내가 보고있는 점에 넣으면 된다.
- 만약 연결된 indegree가 없을 경우, 그 배열엔 0을 넣으면 된다.
- 시간 복잡도는 O(N+M) 이 된다. M은 에지의 개수
정점에 가중치가 있는 그래프 - 동적계획법으로 풀기
- 역시 똑같은 방법으로 dp 배열을 만들어서 푸는 방법 이 있다.
- 인터벌 그래프는 O(N+M) 중 에지가 최대 (n^2-n)/2 일 수 있어서 O(n^2) 이 된다.
- 에지의 개수는 k=1부터 n-1까지 를 모두 더한 시그마 값.
- O(n^2)보다 짧은 경우를 생각해내야 한다.
정점에 가중치가 있는 그래프 - 우선순위 큐를 이용하여 풀기
- 왼쪽점과 오른쪽 점을 다 고려한다. 2n 개의 x좌표를 정렬.
- 아래와 같은 그림일 때, 왼쪽 점을 기준으로 먼저 보게된다. 어떤 구간의 왼쪽 점에 도착하면, 이전까지의 최대 값을 힙에서 꺼내고(힙이 비어있다면 0) 그 구간의 가중치를 더해서 값을 저장 시켜 둔다.
- 어떤 구간의 오른쪽 점에 도착하면 그 이후부터는 그 구간역시 고려되어야 하는 값이 되므로, 힙에 저장시켜둔 값 을 넣는다.
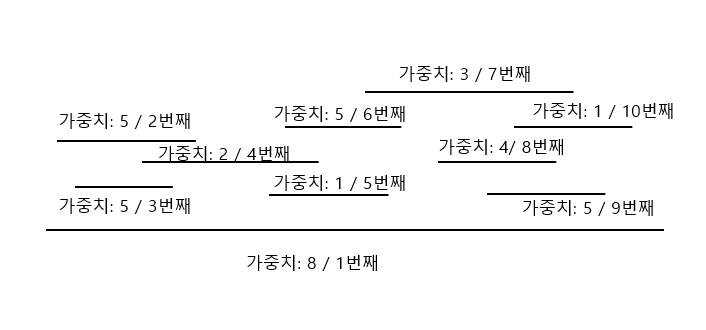
- 맨 처음 첫번째 구간을 보게되면, 가중치 8을 저장시켜둔다.
- 2n개의 좌표들이 정렬되어있으므로 그 다음 보게되는 좌표는 두번째 구간이 된다. 그 구간을 볼때 역시 힙에는 아무것도 들어있지 않으므로, 가중치 5를 저장해 둔다.
- 세번째 구간 역시, 가중치 5를 저장해둔다. 네번째 구간의 왼쪽 점에 도착했을 때도 마찬가지로 가중치 2를 넣어둔다.
- 다음 좌표는 2번째와 3번째 구간의 오른쪽 점 좌표가 된다. 이후부터 나오는 구간들은 두번째 구간과 세번째 구간과 겹치지 않기 때문에, 그 구간들을 포함시킬 수 있게된다. 힙에 2번 구간의 가중치와, 3번 구간의 가중치를 넣는다.
- 다음은 5번째 구간의 왼쪽 좌표가 된다. 왼쪽 좌표 도달 시, 힙에있는 최대 값을 꺼내5번 구간의 가중치를 더한 값을 배열에 저장시켜 둔다.
- 이런 식으로 끝까지 진행하게 되면, 마지막 점을 보게되면 모든 점을 다보게 되는 것이므로, 힙에 있는 최대 값이 정답이 되게 된다.
시간복잡도
- 힙을 이용하는 방식의 경우, 2n개의 좌표만 보면 되고, 힙 내부에선 O(logn) 시간에 최대 값을 찾으므로, O(nlogn) 시간 에 원하는 답을 찾을 수 있게 된다.
- 틀린 부분이 존재할 수 있으니 참고해주시기 바랍니다.
댓글남기기