[알고리즘설계] 정렬의 하계 - 1

2 분 소요

먼저 정렬을 하기 위해서, 정렬을 하기 위한 모든 원소를 한번씩은 탐색하여야 정렬을 할 수 있으므로 직관적으로 n만큼의 시간은 써야된다는 것을 알 수 있다.
그렇다면 하계로 Ω(n)이 된다고 생각해 볼 수 있다.
만약 정렬을 하기위해 n 시간 이상이 필요한 것이 증명된다면 하계의 값이 Ω(n) 보다 큰 하계로 바뀌게 될 것이다.
정렬의 하계 목표는 Ω(nlogn). (비교기반정렬).

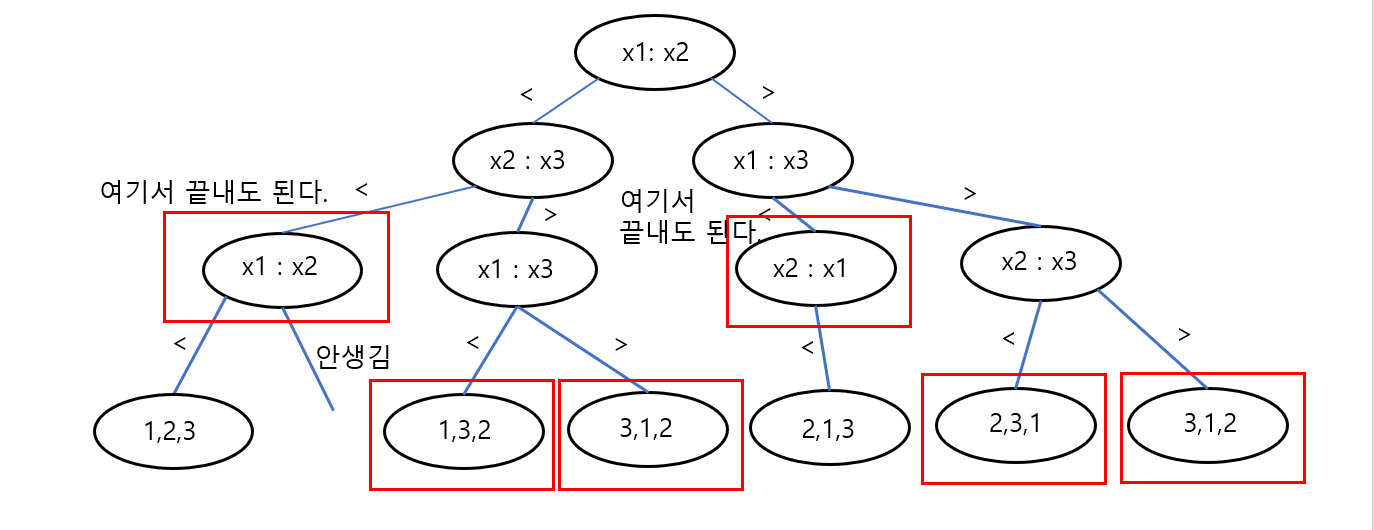
x1,x2,x3 를 버블 정렬로 트리를 구현한다고 하였을 때, 우리는 최악의 경우가 아닌 가장 좋은 알고리즘을 만들어도 최소 이만큼의 시간은 필요하다는 하계에 관심이 있는 것이므로 같은 키 값은 없다고 생각하여도 충분하고, 반복하여 보는 경우 역시 생략해도 충분하다.
3개의 원소를 기준으로 리프노드는 총 6가지가 나온다 (3!, 3개의 원소를 나열할 수 있는 모든 경우의 수).
위의 트리에서 키 값이 같은 경우는 생략하였고, 반복의 경우를 가볍게 줄였을 경우, 위의 리프노드개수처럼 총 6개가 나온다.
하지만 위의 ‘여기서 끝내도 된다’ 라고 쓰여있는 노드들 부분에서 아래로 더 안내려가고 멈춰도 된다. x1과 x2의 비교는 위에서 이미 하였으므로, 이미 저 노드까지 온 경우 x1,x2,x3의 크기비교를 할 수 있기 때문이다. -> 중복제거.

위 그림과 같이 임의의 비교-기반 정렬 알고리즘에 대하여 , 그 알고리즘이 실행하는 비교의 순서를 위와 같은 트리구조로 나타낼 때, 이러한 트리를 “결정트리”라 한다.
결정트리의 조건으로 1) 바이너리 트리, 2) 디그리가 0과 2만 있는 2-Tree 가 있다.
위와 같은 그림에서 3개의 원소로 나열할 수 있는 모든 가지수가 되는 빨간 사각형 노드들(리프노드)을 “External Node” 라고 하고, External Node가 아닌 노드들을 “Internal Node” 라고 한다.

비교, 중복되지 않는 좋은 알고리즘의 트리모양은 2-Tree 모양이 되고, External Node의 개수는 n!이 된다.
이 경우, 비교횟수가 몇번인지 찾아내면 되고 결정트리 모양 중 가장 깊은 레벨에 있는 노드가 정렬이 된 상태일 수 있으므로 External Node의 가장 깊은 레벨이 비교연산횟수가 될 것이다.
비교기반 정렬 알고리즘은 모두 위와 같은 형태의 결정트리 모양이 될 것이고, 만들 수 있는 알고리즘은 무한하고 전부 트리를 만들어 비교하면서 최소를 찾을 수 없으니 이 알고리즘 형태의 결정트리를 만든 것이다.
External Node의 개수를 m으로 정의.
가장 깊은 External Node의 레벨(높이)가 이 알고리즘의 비교연산 횟수가 될 것이다.
높이가 h인 완전 이진트리의 리프노드 개수는 2^h가 되므로, m은 2^h보다 작거나 같게 될 것이다.
m <= 2^h
h >= log(base2)m 이고 m은 n! 이므로, h>= log(base 2) n!이 된다. (계산과정은 로그 부분 포스팅 참조).
즉 위와 같은 모양의 결정 트리(알고리즘)의 최악의 시간복잡도는 O(nlogn)이 될 것이고, 이 시간 복잡도가 비교기반 정렬 알고리즘의 하계가 된다(Ω(nlogn)).

[BOJ12886] 돌 그룹