최소 스패닝 트리 (MST) - 크루스칼

이번 포스팅에서는 최소 스패닝 트리에 대해 다루고, 구현하는 방법에 대해 코드와 함께 설명하도록 한다.

스패닝 트리

• 스패닝 트리가 무엇일까? 스패닝 트리에 대한 정의를 먼저 정확히 내리면서 글을 시작해보자.
• 무향 그래프의 스패닝 트리는 원래 그래프의 모든 정점과 간선의 부분 집합으로 구성된 부분 그래프이다.
• 트리는 그래프의 일종이므로, 부분 그래프라는 말이 이해가 갈 것이다.
• 이때 이 부분 그래프, 즉 스패닝 트리에 포함된 간선들은 정점들을 트리 형태로 전부 연결해야 한다.
• 즉, 간선들이 사이클을 이루지 않는다는 말이다!

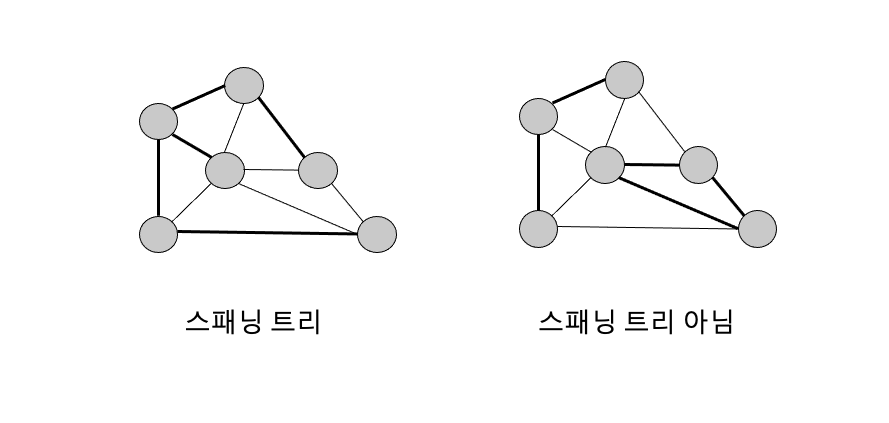
• 왼쪽 그림은 올바른 스패닝 트리이다. 모든 정점으로 이루어져 있고, 굵은 간선이 사이클을 이루지 않는다.
• 반면, 오른쪽 그림을 스패닝 트리가 아니다. 사이클도 아니고, 그래프가 하나로 연결되어 있지 않다.

최소 스패닝 트리란?

• 하나의 그래프에서 스패닝 트리는 여러개가 나올 수 있다.
• 특히, 그래프 중에서 가중치 그래프의 스패닝 트리중에 가중치의 합이 가장 작은 트리가 최소 스패닝 트리(Minimum Spanning Tree)이다.
• 최소 스패닝 트리를 구하기 위한 2가지 알고리즘은 모두 그리디를 바탕으로 이루어져있다.

크루스칼 알고리즘이란?

• 크루스칼 알고리즘은 위에서 말한 것처럼 최소 스패닝 트리를 찾기 위해 그리디하게 가중치가 작은 것부터 추가해 나가는 알고리즘이다.
• 모든 간선을 가중치의 오름차순으로 정렬한 뒤, 스패닝 트리에 하나씩 추가해 나간다.
• 이때, 사이클을 이루면 스패닝 트리가 아니므로, 사이클이 생기는 간선은 제외한다.
• 즉, 가중치가 작은 것부터 하나씩 추가해나가면서 사이클 여부를 확인하는 것이 이 알고리즘의 핵심이다.
• 사이클 생성 확인은 어떻게 할까?

크루스칼 - 사이클 확인

• 첫번째로 사이클을 확인하는 방법은 간선을 하나 추가할 때마다 dfs를 진행하며 백엣지 유무를 확인한다.
• 이 경우는 간선 하나마다(O(E)) dfs(O(N+E))를 진행하므로, O(E^2)의 시간복잡도를 가지게 된다.
• 두번째 방법은 만약 간선을 추가했을 때, 사이클이 생긴다면, 간선의 양 끝 노드가 이미 같은 집합에 속하게 된다.
• 즉, 둘이 같은 집합인지 확인하는 연산과 같은 집합으로 합치는 연산을 빠르게 할 수 있으면 시간복잡도를 줄일 수 있다.
• 결국 유니온 파인드이다!

크루스칼 - 코드 작성 아이디어

• 모든 노드를 처음에는 다른 집합에 속해있게 둔다.
• 1번노드와 2번노드의 간선을 연결할 때, 둘은 초기에 다른 집합에 있으므로, 유니온 연산을 해서 같은 집합에 있게 만든다.
• 2번노드와 3번노드의 간선을 선택한다하면, 역시 2번노드 집합에는 1,2만 있고, 3번 노드 집합은 3번만 있으므로 둘이 초기에 다른 집합에 속해있고, 유니온을 시킨다.
• 이후 만약 1번 노드와 3번노드의 간선을 선택하면, 둘은 이미 같은 집합에 속해있으므로 사이클이 생성된다. 다음 간선으로 넘어가면 된다!
• 이렇게 간선을 선택해나가며, 트리의 간선의 개수인 N-1개까지 선택을 하면 최소 스패닝 트리가 완성이 된다!
• 유니온 파인드 연산의 시간복잡도는 상수시간과 다름없으므로, 트리를 만드는 반복문의 시간복잡도는 O(E)가 된다.
• 결국 전체 시간 복잡도는, 간선을 가중치의 오름차순을 기준으로 정렬을 하기 때문에, O(ElogE), 즉 간선의 개수에 의존적인 시간복잡도를 가지게 된다.

import java.util.*;
import java.io.*;

/**
 * @Author by Sangwoo
 * @Part MST using Kruskal
 */
public class MST_Kruskal {
    private static int V, E;
    private static PriorityQueue<Edge> pq = new PriorityQueue<>((o1, o2) -> Integer.compare(o1.e, o2.e));

    private static class Edge{
        int u, v, e;
        Edge(int u, int v, int e) {
            this.u = u;
            this.v = v;
            this.e = e;
        }
    }

    private static class DisjointSet{
        int[] p;
        DisjointSet() {
            this.init();
        }
        private void init() {
            p = new int[V + 1];
            for (int i = 1; i <= V; i++) {
                p[i] = i;
            }
        }
        private int find(int n) {
            if (n == p[n]) return n;
            return p[n] = find(p[n]);
        }
        private void merge(int n, int m) {
            n = find(n);
            m = find(m);
            p[m] = n;
        }
    }

    public static void main(String[] args) throws IOException {
        input();
        int n = 0;
        int ans = 0;

        // make DisjointSet Instance
        DisjointSet ds = new DisjointSet();

        // loop
        while (!pq.isEmpty() && n <= V - 1) {
            Edge edge = pq.poll();
            if (ds.find(edge.u) != ds.find(edge.v)) {
                ans += edge.e;
                n += 1;
                ds.merge(edge.u, edge.v);
            }
        }
        System.out.println(ans);
    }

    // Input
    private static void input() throws IOException {
        BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(input.readLine());
        V = Integer.parseInt(st.nextToken());
        E = Integer.parseInt(st.nextToken());
        for (int i = 0; i < E; i++) {
            st = new StringTokenizer(input.readLine());
            int n = Integer.parseInt(st.nextToken());
            int m = Integer.parseInt(st.nextToken());
            int w = Integer.parseInt(st.nextToken());
            pq.add(new Edge(n, m, w));
        }
    }
}

정당성 증명 - 귀류법

• 크루스칼이 선택하는 간선 중 최소 신장 트리 T에 포함되지 않는 간선이 있다고 하자. (u-v)
• T는 이 간선을 포함하지 않기 때문에, u와 v는 다른 경로로 연결되어 있다.
• 이 경로에는 (u-v)보다 크거나 같은 간선이 무조건 존재한다.
• 왜냐면, (u-v)보다 모두 작으면, 애초에 (u-v)를 크루스칼이 선택할 일이 없다.
• 이때 이 경로(T에 속해있는) 간선을 하나 지우고 (u-v)를 연결해도 여전히 스패닝 트리이다.
• 그렇다면, (u-v)가 선택된 스패닝 트리의 가중치는 기존 T보다 작거나 같을 것이다.
• T를 최소 스패닝 트리라고 했으므로, (u-v)가 포함된 스패닝 트리도 최소 스패닝 트리가 됨을 알 수 있다.