[자료구조] 머지소트

[자료구조] 머지소트

머지소트란?

• 합병 정렬은 분할 정복 알고리즘 디자인 기법에 근거하여 만들어진 정렬 방법이다.
• 분할 정복의 3단계
  1. 분할 : 해결이 용이한 단계까지 문제를 분할해 나간다.
  2. 정복 : 해결이 용이한 수준까지 분할된 문제를 해결한다.
  3. 결합 : 분할해서 해결한 결과를 결합하여 마무리한다.
• EX) 8개의 데이터를 동시에 정렬하는 것보다, 둘로 나눠서 4개의 데이터를 정렬하는 것이 쉽고, 이들 각각을 다시 한번 둘로 나눠서 2개의 데이터를 정렬하는 것이 더 쉽다.

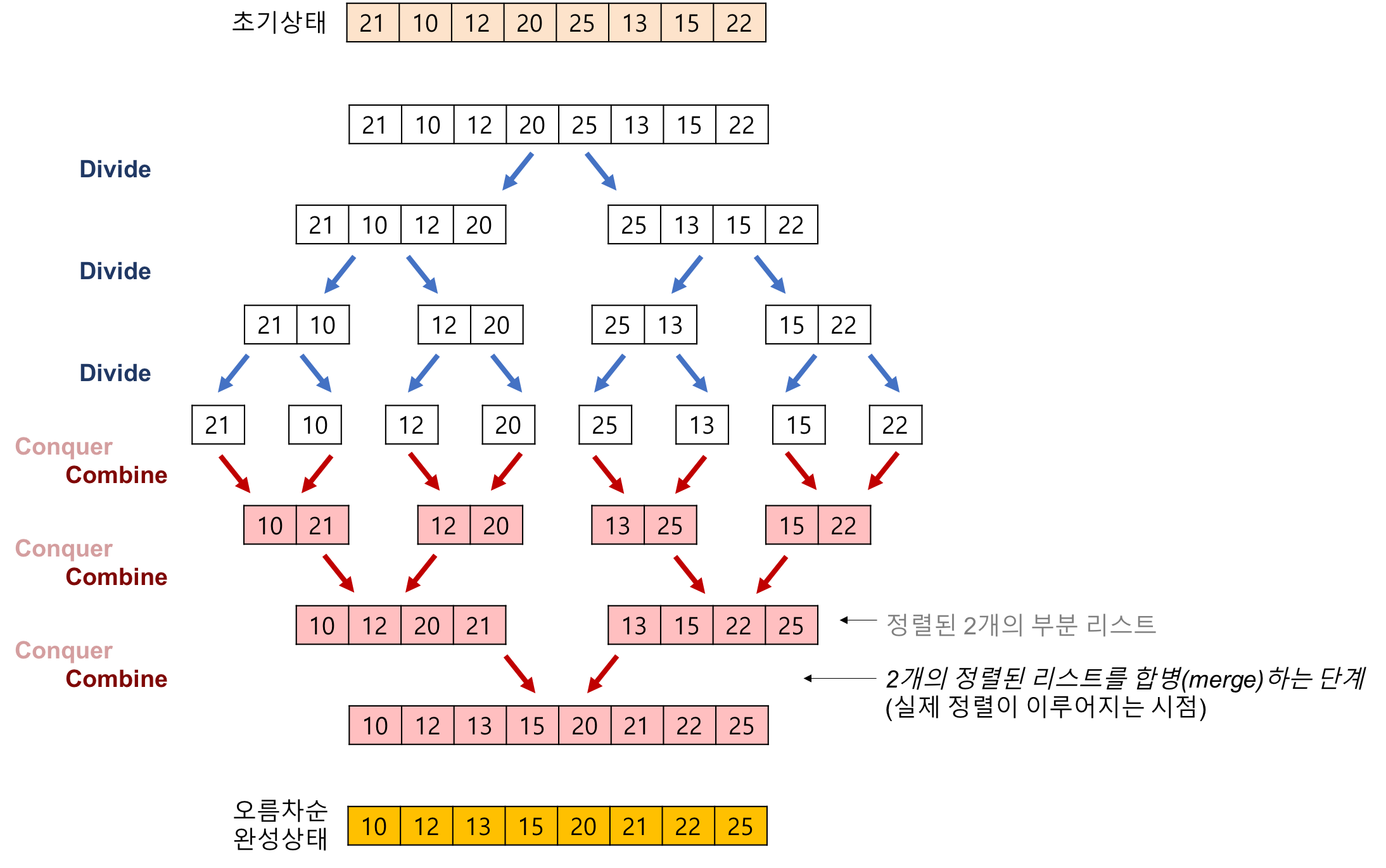
• 사진 출처. https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

• 분할을 할 때에는 위의 그림처럼 정렬을 고려하지 않고 단순히 분할만 하면 된다. (logN)
• 분할이 완료되었으면 병합을 하되, 이제는 정렬 순서를 고려하여 병합시켜준다.

//MergeSort 슈도코드
mergeSort(arr[],l,r){ // arr[l..r]을 정렬한다
    if(l < r){
        mid = (l+r)/2;
        mergeSort(arr, l, mid);
        mergeSort(arr,mid+1,r);
        merge(arr,l,mid,r);
    }
}

merge(arr[], l, mid, r){
    //정렬된 두 배열 arr[l..mid], arr[mid+r..r]을 합병하여,
    //정렬된 하나의 배열 arr[l..r]을 도출한다.
}

• 두 개의 정렬된 배열을 다시 정렬된 하나의 배열로 합병시키는 과정은 간단하다.
• 슈도 코드를 보며 이해해보겠다.

merge(arr[],l,mid,r){ 
    fidx = l; //두개로 나눈 배열 중 첫번째 배열의 첫번째 인덱스
    ridx = mid+1; // 두개로 나눈 배열 중 두번째 배열의 첫번째 인덱스
    k = l;
    temp[] = new [arr.length]; // 정렬된 데이터를 담을 배열을 하나 만들어 준다.
    while(fidx <= mid && ridx <= r){ // 첫번째 배열을 참조할 fidx가 첫번째 배열의 크기보다 작은 동안, 그리고 두번째 배열을 참조할 ridx역시 두번째 배열의 크기보다 작은동안 반복한다.
    // 즉, 병합 할 두 영역의 데이터들을 비교하여 정렬 순서대로 하나씩 temp에 옮겨 담는다.
        if(arr[fidx]<=arr[ridx]){ // 첫번째 배열의 참조된 값과, 두번째 배열의 참조된 값을 비교하여 더 작은 값을 temp 배열에 넣고 인덱스를 한칸 증가시킴. 더 큰 값을 참조하던 인덱스는 그대로 둔다.
            temp[k] = arr[fidx++];
        }
        else{
            temp[k] = arr[ridx++];
        }
        k++;
    }
    if(fidx > mid){ //위의 반복을 끝나고났을 때 두개의 배열 중 하나의 배열은 분명 참조하지 못한 값들이 남아있다. 그 값은 temp배열 뒤에 그냥 붙혀준다.
        for(i=ridx;i<=r;i++){
            temp[k++] = arr[i];
        }
    }
    else{ //위의 if와 같은 과정
        for(i=fidx;i<=mid;i++){
            temp[k++] = arr[i];
        }
    }
    for(i=l;i<=r;i++){ // 정렬된 배열을 원래 배열에 옮겨주면 정렬 완료.
        arr[i]=temp[i];
    }
}

머지소트 시간복잡도

• 머지소트는 분할 정복 과정에서 정확히 n/2 , n/2 로 나누게 된다.
• T(n)을 n개의 데이터를 머지소트하는데 걸리는 시간이라고 정의한다.
• n==1, T(1)=0 (데이터가 1개일 경우는 정렬할 필요 없으므로 0)
• T(n) = T(n/2) + T(n/2) + n(n은 머지하는 데 걸리는 최대 시간)
• 즉, 각 높이마다 n번의 연산이 수행되고, 최대 높이가 logn이기 때문에 O(nlogn)이 된다.