[자료구조] 1.알고리즘 성능분석
[자료구조] 1. 알고리즘 성능분석 방법
1. 알고리즘을 평가하는 중요한 두 가지 요소
- 어떤 알고리즘이 어떠한 상황에서 더 빠르고 또 느린가. -> 속도에 해당하는 알고리즘의 수행시간 분석 결과를 시간 복잡도 라 한다.
- 어떤 알고리즘이 어떠한 상황에서 메모리를 적게 쓰고 또 많이 쓰는가. -> 메모리 사용량에 대한 분석결과를 가리켜 공간 복잡도 라 한다.
2. 공간 복잡도 (Space Complexity)
- 정의 : 프로그램을 실행시켜 완료하는 데 필요로 하는 공간의 양
- 공간복잡도 는 고정 공간 요구 요소와 가변 공간 요구 요소의 합이다.
- 고정 공간 요구 : 프로그램 입출력의 횟수나 크기와 관계없는 공간 요구를 의미.
- 가변 공간 요구 : 특정 인스턴스 I에 의존하는 크기를 가진 구조화 변수들을 위해 필요로 하는 공간들로 구성. 함수가 순환 호출을 할 경우 요구되는 추가 공간을 포함. 인스턴스 I에 작업하는 프로그램 P의 가변 공간 요구는 Sp(I) 로 표기한다. (예를 들어, 입력이 n개의 요소를 갖는 배열이라면 n은 인스턴스 특성이 되어 Sp(n))
- 임의의 프로그램 총 공간 요구 S(P)= c + Sp(I) 이고, c는 고정 공간 요구를 표현하는 상수가 된다. (보통 공간 복잡도를 분석할 때는 가변 공간 요구에만 관심)
- 일반적으로 알고리즘을 평가할 때는 메모리의 사용량보다 실행속도에 초점을 둔다.
3. 시간 복잡도 (Time Complexity)
- 정의 : 프로그램을 실행시켜 완료하는 데 필요한 컴퓨터 시간의 양
- 프로그램 P에 의해 소요되는 시간 T(P) 는 컴파일 시간 과 실행시간 을 합한 것.
- 컴파일 시간 은 인스턴스 특성에 의존하지 않아서 고정 공간 요구 와 유사.
- 알고리즘의 수행속도를 평가할 때는 다음 두 가지 방식을 취한다.
- 연산의 횟수 를 센다.
- 처리해야 할 데이터의 수 n에 대한 연산횟수의 함수 T(n) 을 구성.

- 이 그림을 보면, n이 작은 경우에는 알고리즘 B를, n이 큰 경우에는 알고리즘 A를 써야된다는 생각이 들 수 있다.
- 하지만 데이터의 수가 적은 경우의 수행속도는 의미 없고, 중요한 것은 데이터의 수가 많아짐에 따른 연산 횟수의 증가 정도 에 있다! 즉, 알고리즘 A가 훨씬 시간복잡도가 작은 좋은 알고리즘
4. 빅-오 표기법(Big-Oh Notation)
- 빅-오라는 것은 함수 T(n)에서 가장 영향력이 큰 부분을 따지는 것.
- 빅-오의 수학적 정의 : 두 개의 함수 f(n)과 g(n)이 주어졌을 때, 모든 n>=K에 대하여 f(n)<=C * g(n)을 만족하는 두 개의 상수 C와 K가 존재하면, f(n)의 빅오는 O(g(n))이다.
- 빅오에서 중요한 것은 단순히 f(n)<=C * g(n)을 만족하는 n값이 아닌, n의 값이 커지면서 어느 순간부터는 f(n)<= C * g(n) 을 항상 만족해야 한다는데 있다.
- 즉, 5n^2+100 의 빅오는 O(n^2)이 되고, 이 말은 증가율의 패턴이 n^2을 넘지 못한다는 것.
- 빅-오의 정의 : 데이터 수의 중가에 따른 연산횟수의 증가율의 상한선을 표현한 것
- T(n)이 다항식으로 표현된 경우, 최고차항의 차수가 빅오가 된다.
- T(n)= n^2+2n+9 -> O(n^2)
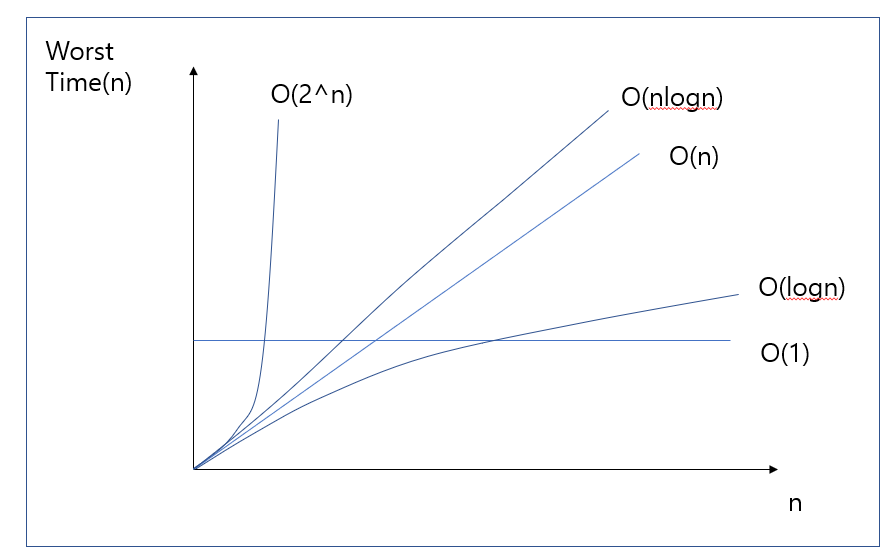
5. 대표적인 빅오
- O(1) : 상수형 빅오(n에 상관없이 연산횟수가 고정)
- O(lgn) : 로그형 빅오(데이터 수의 증가율에 비해 연산횟수 증가율이 훨씬 낮은 알고리즘)
- O(n) : 선형 빅오(데이터의 수와 연산횟수가 비례)
- O(nlgn) : 선형로그형 빅오(데이터 수가 2배로 늘 때, 연산횟수는 두 배 조금 넘게 증가)
- O(n^2) : 제곱에 해당하는 연산횟수를 요구하는 알고리즘
- O(2^n) : 지수형 빅오(사용하기엔 무리. 지수적 증가)
오메가와 세타에 대해선 조만간..
참고 문헌
1. 윤성우의 열혈 자료구조
2. C로 쓴 자료구조론
댓글남기기