[자료구조] 퀵소트

[자료구조] 퀵소트

퀵소트란?

• 퀵소트 역시 머지소트처럼 분할 정복 방법 을 이용하여 구현된다.
• 퀵소트의 시간복잡도는 평균적으로 O(nlogn) 그리고 최악의 경우 O(n^2) 을 가진다.
• 퀵소트의 평균시간복잡도에 대한 증명은 https://sangwoo0727.github.io/algorithm/Algorithm-QuickSortAve/ 이 포스팅에 정리를 해놨었으므로 참고해주시면 됩니다.
• 최악의 경우 O(n^2)인데 왜 이름부터 퀵소트냐고 하면 설계를 통해 최악의 경우는 개선이 가능한 부분이기 때문이다.
• 이 포스팅의 아래 부분에선 개선방안에 대한 글을 작성하겠다.

퀵소트 구현방법

• 피벗을 통하여 기준을 잡게되는데, 피벗은 중심축 이라는 의미를 담고있다.
• 피벗은 정렬하는데 필요한 일종의 기준이라고 생각하면된다.
• 예를 들어 가장 왼쪽에 위치한 데이터를 퀵 정렬에 필요한 피벗으로 정할 수 있다. 즉 설계하는 사람의 결정에 따라 피벗이 정해지는 것이다.
• 가장 왼쪽에 위치한 데이터를 피벗으로 가정할 때, low는 피벗을 제외한 가장 왼쪽에 위치한 지점을 가리키는 변수로 설정, high는 피벗을 제외한 가장 오른쪽에 위치한 지점을 가리키는 변수로 설정한다.
• low는 오른쪽으로 피벗보다 큰 값을 만날때까지, high는 왼쪽으로 피벗보다 작은 값을 만날때까지 이동한다.(일반화 시키면 low는 피벗보다 정렬의 우선순위가 낮은 데이터를 만날때까지, high는 정렬의 우선순위가 높은 데이터를 만날때까지)

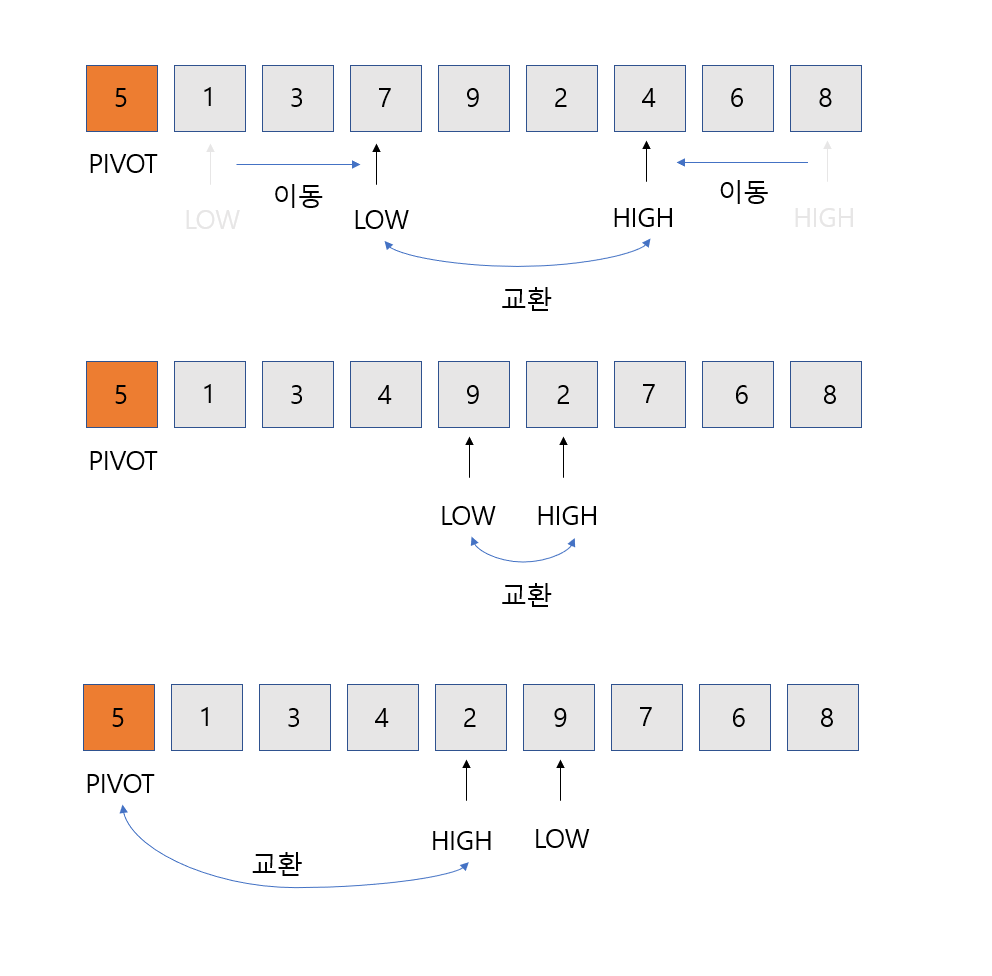
• 그림으로 표현해보았다.

// 퀵소트 피벗을 기준으로 왼쪽,오른쪽으로 나누는 partition 함수

int partition(int arr[],int left,int right){
    int pivot = arr[left];
    int low = left+1;
    int high = right;

    while(low <= high){
        while(pivot > arr[low]) low++;
        while(pivot < arr[high]) high--;
        if(low <= high) swap(low,high);
    }
    swap(left, high);
    return high; // 피벗의 위치가 반환됨.
}

• 이 함수가 끝나고 나면 반환되는 값은 제 자리를 찾은 피벗의 인덱스 값이다.
• 다음은 위의 함수를 포함한 퀵소트의 알고리즘이다.

void QuickSort(int arr[],int left,int right){
    if(left <= right){
        int pivot = partition(arr,left,right);
        QuickSort(arr,left,pivot-1);
        QuickSort(arr,pivot+1,right);
    }
}

퀵소트의 성능 평가

• 퀵소트의 시간복잡도는 아까 말한것처럼 위의 포스팅을 참조하면 된다.
• 지금부터는 퀵소트의 최악의 시간복잡도를 방지하여 설계하는 방법에 대한 내용이다.

퀵소트의 최악의 경우(O(n^2))을 방지하기 위한 설계 방법.

1. 배열의 랜덤화 (출처 : The Algorithm Design Manual)

• 배열의 랜덤화 는 가장 쉬운 방법이다.
• firstPivotQuickSort를 그대로 사용할 수 있다.

void make_random_array(int *arr){
    for(int i=0;i<MAXN;i++){
        swap(arr[rand() * rand() % MAXN],arr[rand() * rand() % MAXN]);
    }
}

• 위의 코드를 전처리 해줌으로써 배열의 랜덤한 두 인덱스의 원소를 뒤바꾸어주는 방식으로 O(n)만큼의 전처리시간 이 추가될 뿐이다.
• 완전한 완벽한 방식이라고는 할 수 없지만 충분히 배열을 섞어줄 수 있다고 생각한다.

2. 랜덤한 피벗 선택

• 피벗을 기존처럼 맨 앞의 원소로 선택하지 않고, 난수를 발생시켜 선택하는 방법 이다.
• 1번의 랜덤화와 명확한 차이점은 1번의 경우 첫번째 원소를 계속해서 피벗으로 고르되 배열 자체를 랜덤화 시켜주는 방법이고, 이 경우는 배열은 그대로 두되 피벗을 랜덤하게 선택하는 방법이다.
• 퀵 정렬에서 최악의 피벗을 뽑을 확률은 2/n이다.(가장 작은 숫자나 가장 큰 숫자를 뽑을 확률)
• 만약 난수를 발생시켜 피벗을 고르게된다면 2/n확률로 계속해서 최악의 피벗을 뽑을 확률은 매우 작을 것이다.

3. Median of Three Pivot

• 임의로 피벗을 한 원소로 선택하는 것이 아닌, 3개의 원소를 후보로 두고 그 중간 값을 선택하는 방법
• 이런 경우엔 차악이 선택될 순 있지만, 최악이 선택되진 않을 것이다.

int findMedianPivot(int arr[],int a,int b, int c){
    int pivot = (arr[a]+arr[b]+arr[c])- max({arr[a],arr[b],arr[c]}) - min({arr[a],arr[b],arr[c]});
    return pivot == arr[a] ? a: pivot==arr[b]? b: c;
}

• 3개의 원소 중 중간 값은 a+b+c - 세 원소중 최대 - 세 원소중 최소이다.