[알고리즘설계] Interval Graph - 2 (Scheduling)

[알고리즘 설계] Interval Graph - 2 (Scheduling)

---

문제

• Interval Graph - 1 에서 주어졌던 구간들을 이번에는 스터디룸 예약시간으로 생각해보자. 스터디룸의 예약 시작시간과 끝나는 시간을 구간의 시작점과 끝점으로 주어졌을 때, 이번에는 최소 몇 개의 스터디룸을 할당하면 모든 예약시간(구간)이 다 들어갈 수 있는지를 구하는 문제이다.

---

문제 해석

• Interval Graph - 1 문제와 다른 점은 앞의 문제의 경우 부분집합들 중 크기가 가장 큰 부분집합을 구하는 것이지만, 이번 문제는 모든 구간들을 부분집합에 넣을 때, 교집합이 없이 만들 수 있는 부분집합의 최소 개수 를 구하는 문제이다.

• 전체 Interval 들의 집합 : A .

• A = A1 ∪ A2 ∪ A3 …… ∪ Ak , 서로 다른 i와 j에 대해 Ai ∩ Aj = Φ(공집합).

• 즉 , 서로 다른 집합들 사이엔 교집합이 없다.

• 이 문제는 결국 ‘분할(Partition)문제’가 된다. (두 곳에 속하는 경우 없음).

---

문제를 풀기위하여 생각해볼 수 있는 방법들.

1. 첫번째 방에 넣을 수 있는 최대의 개수를 넣고 두번째 방에 또 최대로 넣는 식으로 진행하는 방법

• 이 경우 항상 방의 개수가 최대가 될까?

• 반례.

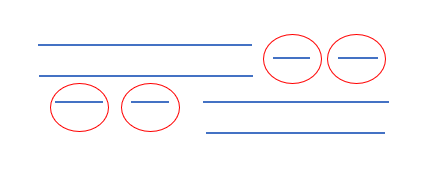
• 아래 그림의 경우, 빨간 동그라미가 쳐진 작은 구간 4개가 전부 한 방에 들어간다.

• 그 후, 나머지 네개의 구간이 모두 겹치므로 각각 한개의 방씩 배정이 되어 총 5개의 방을 할당하게 된다.

• 하지만 저 그림에서 방의 최소 개수는 4개가 된다. (금방 찾을 수 있다.)

2. 동시에 겹치는 구간의 개수가 가장 많을 때(임의로 동시에 겹치는 구간의 개수를 M-number라고 지칭)의 개수만큼 할당하면 될까?

• 가장 많이 겹치는 구간의 개수, 즉 M-number가 가장 클 때 , 그 M-number가 정답인 방의 최소의 개수가 되는지 구해보려는 것.

• M-number가 1일 때는 모양이 ㅡ ㅡ ㅡ ㅡ ㅡ ㅡ 이런식으로 생길테니 필요한 방의 개수는 1개가 될 것이다.

• M-number가 2 이상일 때, 위의 주장을 만족하려면 M-number 부분에 존재하고 있는 구간 한개를 방에 넣어서 방 개수 한개를 줄어들게 해야 한다. (M-number 구간에서 뽑지 않을 경우, 그 구간이 들어간 방의 개수 + M-number 만큼 방을 더 할당해야 해서 모순이 생긴다).

• 아래는 위의 주장이 맞는지 확인하는 과정.

• A가 다음 M-number 구간(2번구간) 을 지나는 구간일 경우, 방에 넣었을 때 2번 구간의 M-number 역시 줄어들기 때문에 성립한다.

• A가 2번구간보다 전에 끝날 경우에는 2번 구간에 있는 스케쥴이 A와 2번 구간이 아닌 곳에서 겹치게 되고, A와 겹치지 않는 구간이 무조건 1개 이상 존재 하게 된다.

• 그러므로, n=1 일때는 1개가 되고, n>= 2 일때는 , 가장 큰 M-number 구간들을 구하고, 그 구간들 중 하나의 interval을 사용하여 방을 만들고, 그 다음 interval들 중 겹치지 않는 interval을 고르는 식으로 해결하면 된다.

• 하지만 이 알고리즘보다 훨씬 속도가 빠른 알고리즘이 존재한다.

3. 왼쪽 끝점부터 보면서 “아무 방이나 들어가세요” , 라고 한 뒤 “방이 없으면 새로 만들고 들어가세요” 라는 방식으로 푸는 방법.

• 힙을 이용하여 풀되, 어떤 구간 먼저 힙에 넣을지 보는 것은 왼쪽 시작점이 빠른 순 으로, 힙에 들어가는 값은 오른쪽 끝점 이 들어간다.

• 다음 값의 왼쪽 점이 힙에 있는 값보다 클 때, 힙의 맨 앞을 삭제하고, 다음 구간의 오른쪽 끝 값을 넣는다. 다음 값의 왼쪽점이 힙에 있는 최소값보다 작을 땐, 삭제 없이 추가만 한다.

• 힙에는 다음 구간의 왼쪽 점이 힙에 있는 값(앞 구간들의 오른쪽 끝 값)보다 클 경우에만 삭제하고 추가하는 과정이 들어가게 되서, 추가로 들어오는 것이 없으면 기존에 힙에 있는 값은 삭제되지 않는다.

• 그러므로 마지막 구간까지 탐색이 끝난 후, 힙에 남아있는 값의 개수 가 그대로 최소 방의 개수가 된다.

• 아래 그림으로 살펴보자

1. 힙에 1번 구간의 오른쪽 점 값 이 들어간다.
2. 힙에 있는 값보다 2번 구간의 왼쪽 점이 작으므로 힙에 2번 구간의 오른쪽 점이 추가 된다.
3. 3번의 왼쪽 점이 힙에 있는 최소 값보다 크므로, 1번 구간의 오른쪽 끝점이 삭제되고 3번 구간의 오른쪽 끝점이 추가된다.
4. 4번의 왼쪽 점은 힙에 있는 값들보다 작으므로 힙에 4번 구간의 오른쪽 점이 추가 된다.
5. 5번 역시 4번과 같은 이유로 힙에 오른쪽 점이 추가 된다.
6. 6번 구간의 왼쪽 점이 힙에 있는 최소값보다 크므로, 4번 구간이 삭제되고 6번 구간의 오른쪽 끝점이 추가 된다.
7. 7번 구간역시 힙의 최소값보다 크므로 2번 구간이 삭제되고 7번 구간의 오른쪽 끝 점이 추가 된다.
8. 8번 구간 역시 힙의 최소값이 삭제되고 8번구간의 오른쪽 끝점이 추가 된다.
9. 마지막으로 힙에 남아있는 값의 개수를 구하면 총 4개 가 된다.

---

• 틀린 부분이 존재할 수 있으니 참고해주시기 바랍니다.